R/Pharma Workshop on Multistate Modeling

R in Pharma workshop

Juho Timonen and I held a workshop on multistate modeling as part of the R/Pharma virtual conference last week. Approximately 50 people attended, and we covered both a canonical example of multistate modeling (the Cardiac Allograft Vasculopathy or cav dataset) and an analysis of oncology data from the control arm of the SQUIRE trial, based on data included in the supplement to a recent publication by Lin et al (2024) [1].

The materials from the tutorial are now available on our github repository: https://github.com/generable/r-pharma-bmstate

I had a lot of fun putting this material together. In this post, I will describe the SQUIRE data analysis we presented there, as this was my focus.

‍

SQUIRE data

This was a Phase III trial in treatment-naive stage IV squamous non-small-cell lung cancer patients. The active control arm received up to 6 three-week cycles of gemcitabine and cisplatin therapy between 2010 to 2012. There were approximately 550 subjects in the released data.

Since I had effectively a single arm to analyze, I decided to lean into the simulation capabilities of Juho's bmstate package [2] to first fit a model to the control-arm data and then use the posterior estimates of parameters to simulate data for various treatment effects.

The key question I focussed on was:

How strong of a treatment effect would be required to impact overall survival, if a treatment impacted only response directly?

The data, as prepared, include 6 event-states, where "no-progression" refers to a subject reaching the end of tumor-size data collection without evidence of disease progression:

We can visualize individual paths of particular subjects as follows. Each row is a subject:

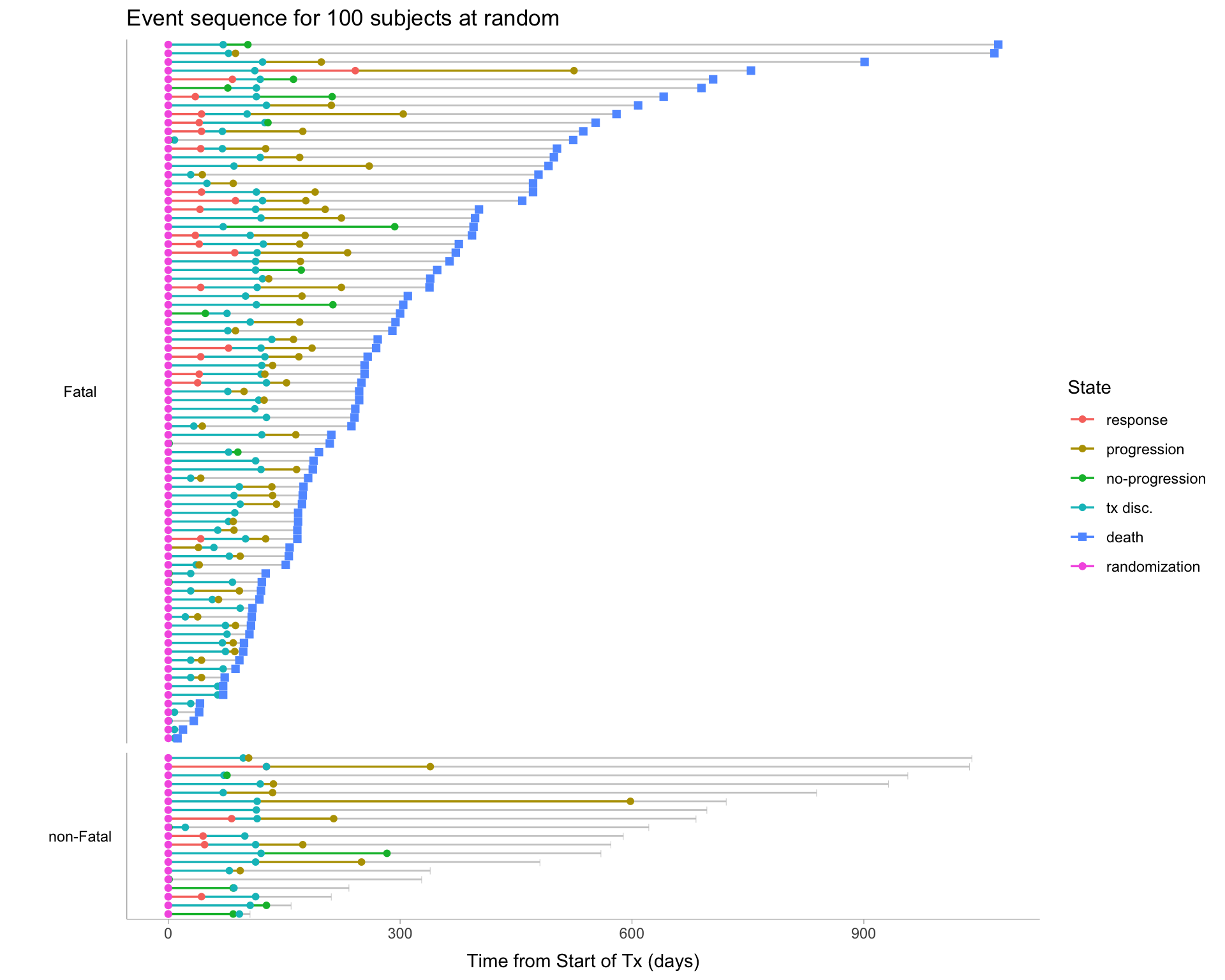
Even from this plot, a few patterns are clear:

1. There is, unfortunately, a high fatality rate for this population
2. The most common sequence of events is response -> tx disc -> progression -> fatality.
3. It's not clear how important "response" is to the overall trajectory

‍

First model fit

We start with a simplified version of the event graph, including the 4 most impactful states for subject outcomes.

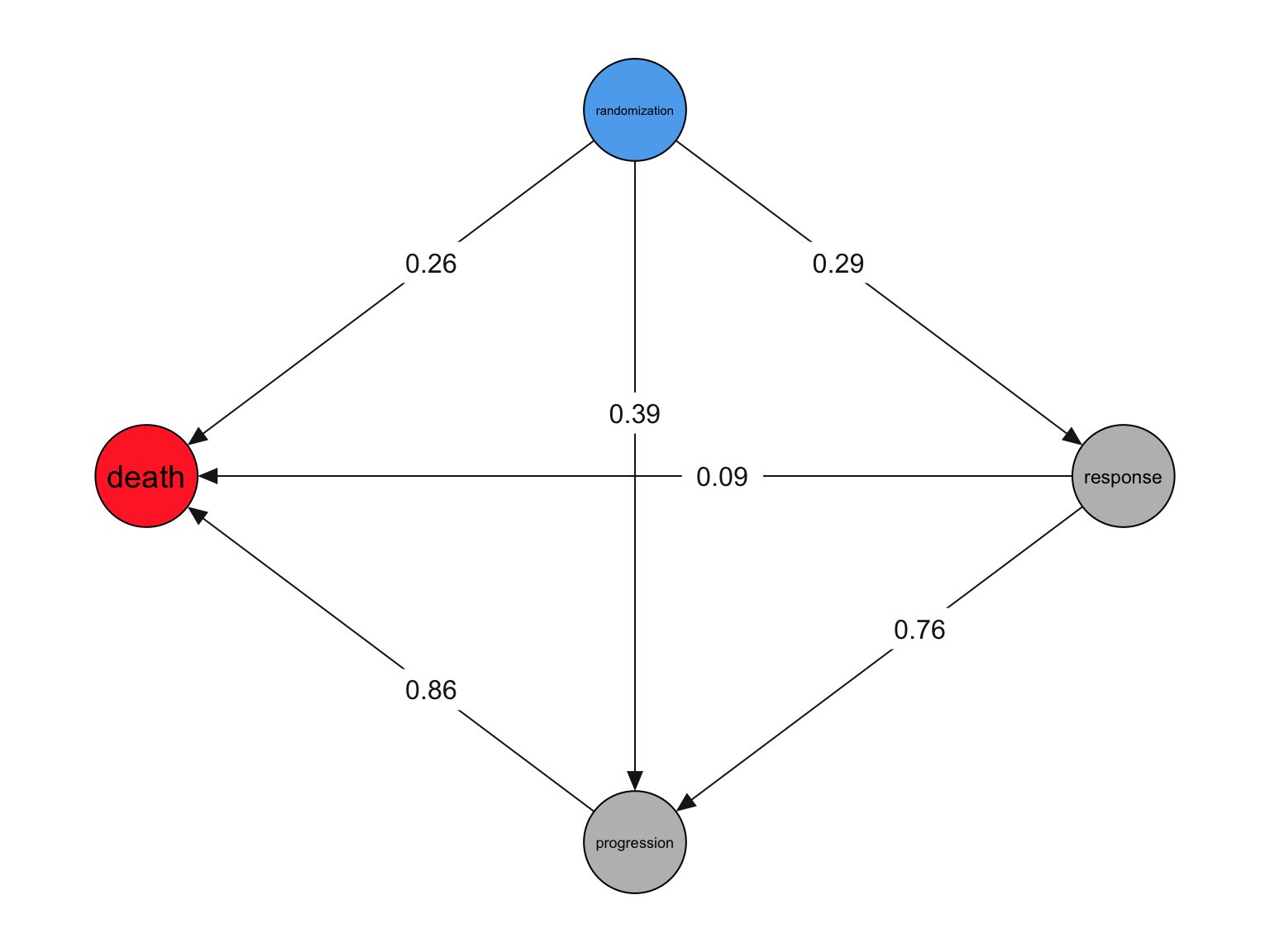
These numbers show the raw, observed transition rates from each state to the next. In other words, 29% of patients in the "randomization" state are in the "response" state following randomization.

A few observations:

1. These numbers corroborate our impression from the data exploration regarding the high fatality rate in this population.
2. Transitions from the initial state seem evenly split between all three states. Approximately 26%, 39% and 29% transition to fatality directly, progression directly, or response, respectively.
3. However, after this initial state, the transition path tends to follow the response -> progression -> fatality path.

Our first model fit includes these 4 states, and shows very good sampling characteristics -- the full analysis script is included in the repository. For simplicity we include only a single baseline covariate: ECOG score.

Note that ECOG score measures how mobile and self-sufficient a subject is, with higher values reflecting worse health. More details here.

‍

Simulating data

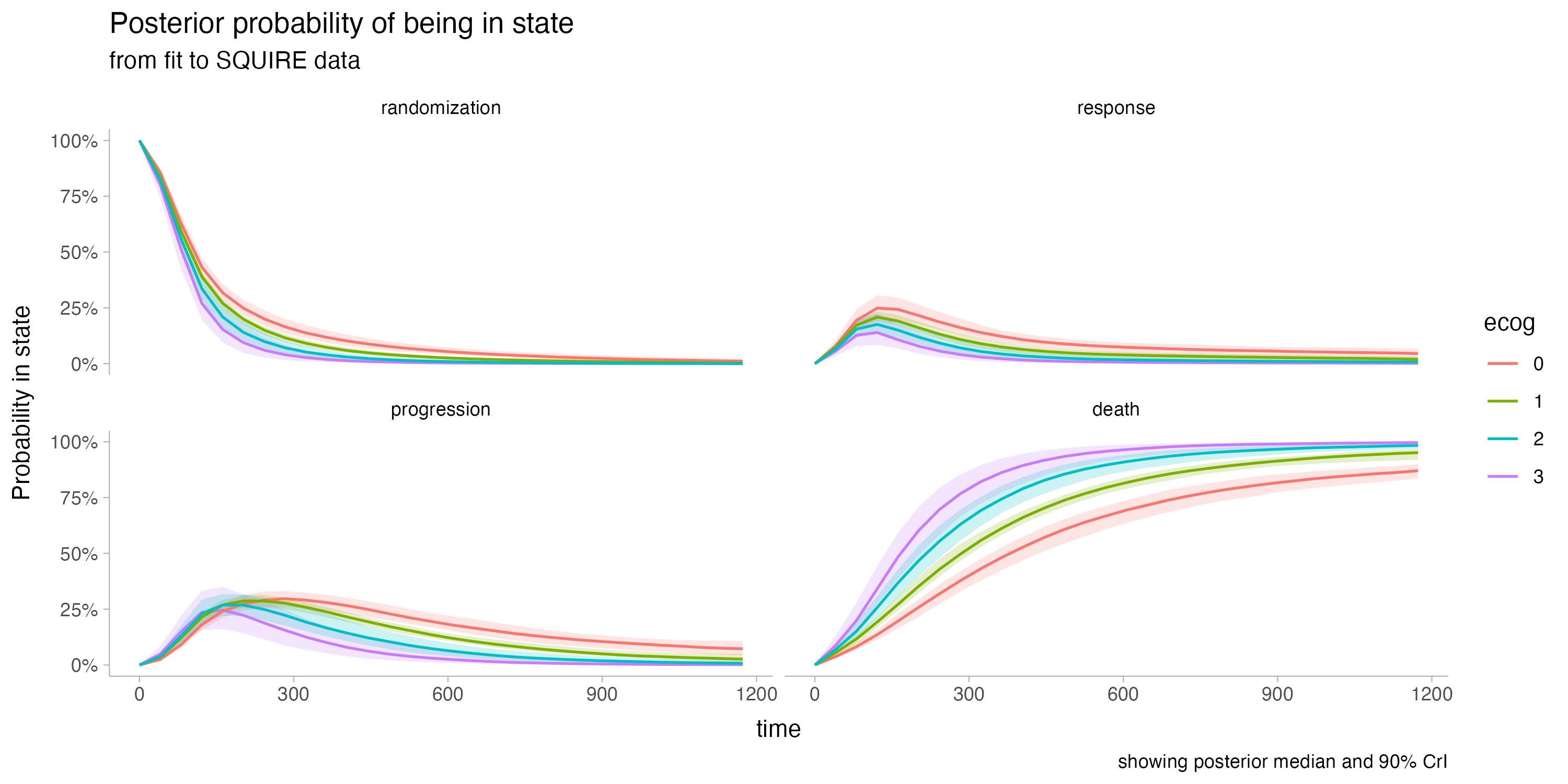
We then use this fit to simulate data with a treatment effect, given the estimated parameters (baseline hazards plus covariate effects).

We simulate a treatment effect on response of 0.2, _equal to a one-unit change in ECOG_. This is a pretty strong treatment effect.

First, I want to point out how relatively easy it is to simulate data given a model fit:

simd2 <- mod1$simulate_data(
  N_subject = 550,
  beta_haz = tx_effects |> select(beta_ecog, beta_tx) |> as.matrix(),
  w = fit0_w[1, 1, , ],
  w0 = fit0_w0[1, 1, ]
)

note: full details are in the code examples

Of course, I have to point out that the model is able to recover the true values used to simulate the data quite well:

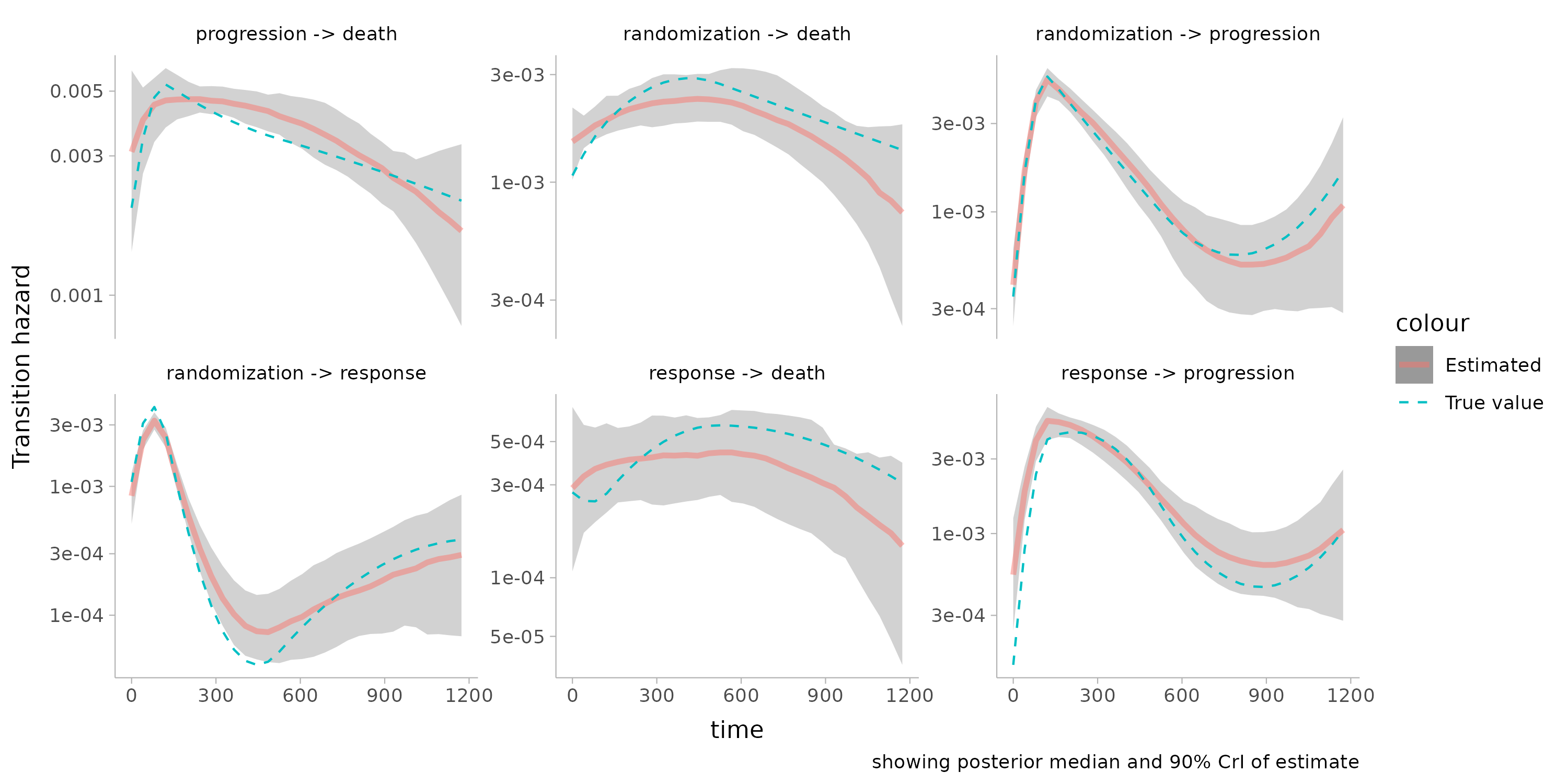
In addition, we found that this treatment effect is unlikely to meaningfully impact overall survival

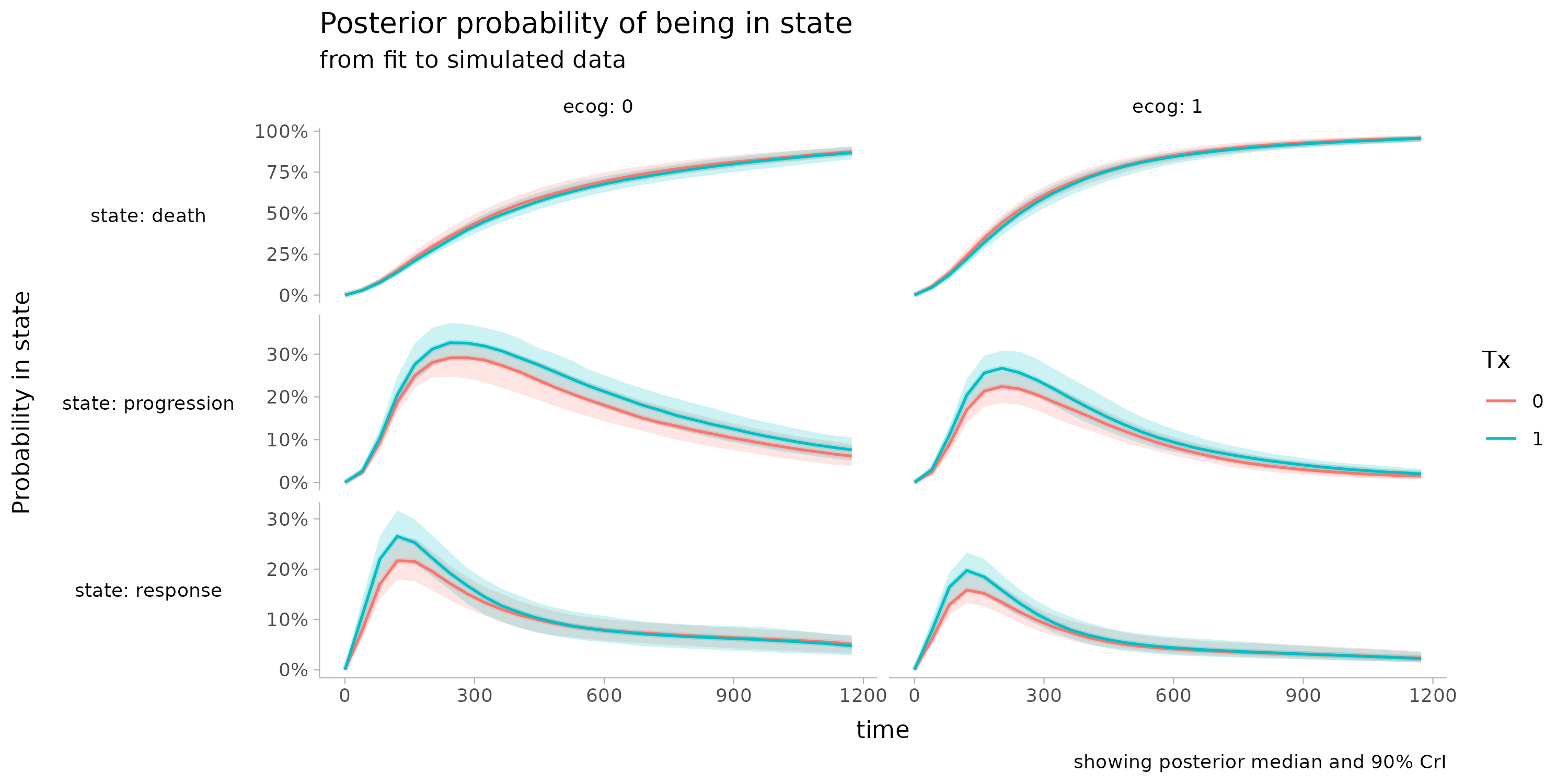
This seems obvious in retrospect -- the progression and fatality rates are so high in this population that a slight increase in response would be unlikely to have an effect -- but it's jarring to see it so clearly. This would be an interesting analysis to repeat among a greater variety of treatments.

‍

Conclusions

In short, I had a lot of fun putting together the code examples for this tutorial. Thanks to the organizers and participants for a great event.

Happy modeling!

References

[1] Lin C‐W, Nagase M, Doshi S, Dutta S. A multistate platform model for time‐to‐event endpoints in oncology clinical trials. CPT Pharmacometrics Syst Pharmacol. 2024;13:154‐167. doi: 10.1002/psp4.13069

[2] Timonen J (2025). bmstate: Bayesian multistate modeling. R package version 0.2.2, commit 18fba62575b608f138e3dcc0c1bce1de7f9ee498,
 <https://github.com/generable/bmstate>.

‍